我们需要为重建的人头添加一个背景。其中一个方案是，直接找到一张全景图，背景、光照都从全景图中来。

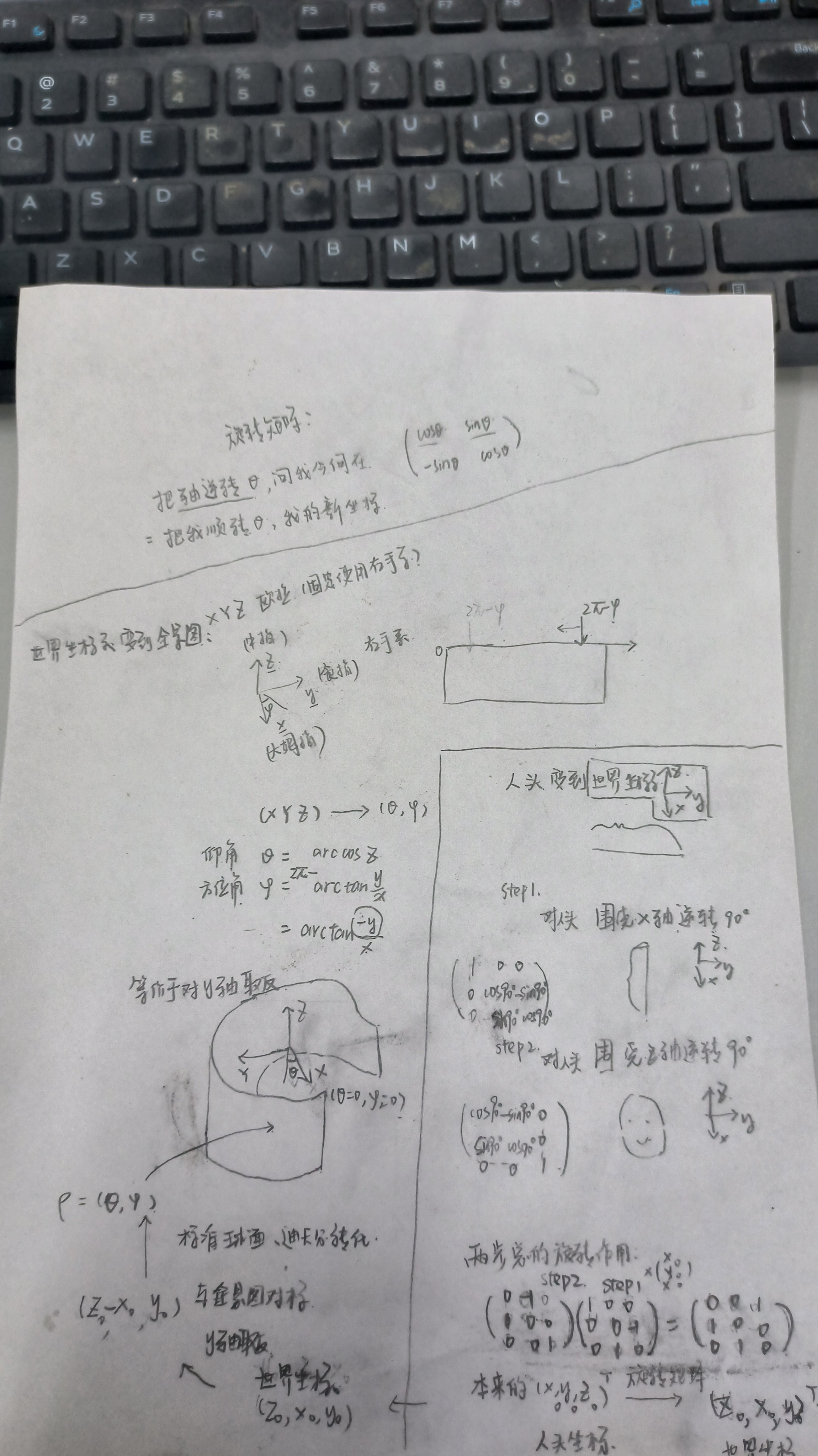
球面坐标与欧式坐标之间的转化

从全景图中采样出背景图，这个过程涉及到球面坐标和标准欧式坐标之间的转换。

查阅资料后，我了解到球面坐标系与标准欧氏坐标系之间（空间直角坐标系）之间有固定的转化公式。球极坐标中的仰角、方位角在标准欧式坐标中怎么画，都是有规定的。

仰角-方位角

在全景图中，假如采用“仰角elevation-方位角azimuth”的方式确定像素的位置，那么使用上述标准的转换公式即可。例如，EMLight里有这样的写法：

# 笛卡尔坐标系（标准欧氏坐标系、空间直角坐标系）->极坐标（球面坐标系）
def cartesian_to_polar(xyz):
    theta = np.arccos(np.clip(xyz[2], -1.0, 1.0))
    phi = np.arctan2(xyz[1], xyz[0])
    return phi, theta
    # return np.stack((phi, theta), axis=1)

# 极坐标（球面坐标系）-> 笛卡尔坐标系（标准欧氏坐标系、空间直角坐标系）
def polar_to_cartesian(phi_theta):
    x = np.sin(phi_theta[:, 1]) * np.cos(phi_theta[:, 0])
    y = np.sin(phi_theta[:, 1]) * np.sin(phi_theta[:, 0])
    z = np.cos(phi_theta[:, 1])
    return np.stack((x, y, z), axis=1)

由于仰角和方位角经常用$\theta$和$\phi$表示，代码里经常用theta和phi代指仰角和方位角。

经度-纬度

但也有的时候，全景图被看成一张世界地图，以经纬度标记像素位置。
全景图拍摄时,相机往往将镜头对准正北方向进行拍摄。此时,图片的正中央对应地理坐标的北纬方向,经度为0度。

随着视角向东移动,经度值逐渐增加;向西移动,经度值逐渐减小。当视角转到正南方向时,经度达到最大值180度或最小值-180度。

所以在全景图中,不管相机的朝向如何,经度为0的位置通常都在图片的正中央,表示北纬方向。这与我们平时看地图的习惯也是一致的。
所以，在经纬度描述的全景图中，中心位置才是O点，经度纬度都是0。左上角是成了纬度为90度,经度为-180度的点。此时代码里常用经纬度的英文，即Longitude and latitude。以下是来自Stack Overflow的代码，将经纬度转笛卡尔。可以看到，其与上面一种“仰角-方位角”的主要区别就在于，套在lat外的sin和cos是相反的。

# Converting lat/long to cartesian
import numpy as np

def get_cartesian(lat=None,lon=None):
    lat, lon = np.deg2rad(lat), np.deg2rad(lon)
    R = 6371 # radius of the earth
    x = R * np.cos(lat) * np.cos(lon)
    y = R * np.cos(lat) * np.sin(lon)
    z = R *np.sin(lat)
    return x,y,z

反转可以这样写：

# 三维空间坐标到经纬度坐标的转换函数
def xyz2polar(xyz):
    lat = np.arcsin(xyz[2])
    lon = np.arctan2(xyz[1], xyz[0])
    return np.array([lon, lat])

当lat和lon都为0时，xyz=[1,0,0]。

相机成像过程中的多个参考坐标系

从全景图采用背景，需要知道相机在世界坐标系中的朝向；根据人头表面法向采集光照，也需要知道人头坐标系中的法向如何转化到世界坐标系中。
首先，应当明确，相机拍照的过程，是把世界坐标系中的点捕获到相机坐标系，再通过凸透镜投影到像平面上，最终放到像素平面上的。

相机的内参和外参矩阵表明了如何做这一系列转化。

外参矩阵

外参矩阵worldToCamera，能够将世界坐标系中的点$P^W$的坐标转成相机坐标系中的坐标$P^C = P^W * worldToCamera$。外参矩阵是4$ \times$4的矩阵，左上角的3$ \times$3负责旋转，最后一列负责平移。在三维重建中，可能外参矩阵的逆矩阵cameraToWorld更有意思。它能把相机坐标系中的点放回世界坐标系中。同时，它的前三列分别对应$cameraToWorld * [1,0,0]^T$、$cameraToWorld * [0,1,0]^T$、$cameraToWorld * [0,0,1]^T$的结果，即相机坐标系xyz三个轴在世界坐标系中的真实指向。cameraToWorld的第四列则直接表明相机在世界坐标系中的位置。
下面这个函数是个例子，讲述如何从外参矩阵中提取这些有用信息。外参矩阵暗示相机在世界坐标系中的位置和朝向，因而这个函数名为setCameraPose，即和相机的Pose有关。

# 根据相机外参矩阵设置相机参数
def setCameraPose(self, cameraToWorld):
    """
    worldToCamera，cameraToWorld: 4x4 matrix
    相机外参矩阵worldToCamera，即世界坐标系到相机坐标系的变换矩阵，P^C = P^W * worldToCamera
    cameraToWorld，即相机坐标系到世界坐标系的变换矩阵，P^W = P^C * cameraToWorld
    cameraToWorld的第四列为相机在世界坐标系下的坐标，即相机的位置
    cameraToWorld的第三列为相机在世界坐标系下的朝向，即相机的朝向
    cameraToWorld的第二列为相机在世界坐标系下的上方向，即相机的上方向
    cameraToWorld的第一列为相机在世界坐标系下的右方向，即相机的右方向
    """
    self.cameraToWorld = cameraToWorld
    self.cameraPosition = cameraToWorld[:3,3]
    self.cameraOrientation = cameraToWorld[:3,2]
    self.cameraUp = cameraToWorld[:3,1]
    self.cameraRight = cameraToWorld[:3,0]
    self.worldToCamera = np.linalg.inv(self.cameraToWorld)

    self.cameraToWorld = np.expand_dims(self.cameraToWorld, axis=0)    
    self.worldToCamera = np.expand_dims(self.worldToCamera, axis=0)
    self.cameraPosition = np.expand_dims(self.cameraPosition, axis=0)
    self.cameraOrientation = np.expand_dims(self.cameraOrientation, axis=0)
    self.cameraUp = np.expand_dims(self.cameraUp, axis=0)
    self.cameraRight = np.expand_dims(self.cameraRight, axis=0)

相机坐标系中z轴的朝向一般就是相机的朝向，而外参矩阵的第三列就是我们需要的相机在世界坐标系中的朝向。

内参矩阵

外参指的是相机与外部世界之间的关系，内参则决定相机坐标系中的点如何变化到像平面、像素平面上。这部分的变换都是二维上的变换，主要用到三角形相似定理。相机坐标系中的任意一点(x,y,z)，等比例相似变换到像平面中，成了(x’,y’,f)。$f$是焦距。x’,y’,f的单位就是真实世界里的长度单位，只不过比米小很多，一般是毫米。
$$
x/x’ = y/y’ = z/f
$$

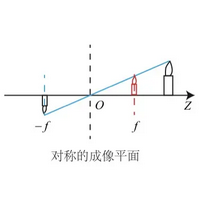
然而，像平面上的图像，最终要转化成像素组成的像素平面上（即最终看到的图像）。此时有是一次等比例放缩，数值放缩多少由传感器中一个像素的长和宽决定。像素越小，则同样的像平面最终获得的像素图越大。此时，还要把原点从光心挪到图片左上角。最终的像素图为(u,v):
$$
u = \alpha x’ + c_x = \alpha xf/z + c _x ;\
v = \beta y’ + c_y = \beta yf/z + c_y
$$
$c_x、c_y$的单位都是像素，即光心在像素图上的位置，一般是像素平面长和宽的一半。原先的$f/z$用于将相机坐标系中的点放缩到像平面中。这里又额外有了像平面到像素的放缩因素$\alpha$，因此可以把这两个放缩因素打包成$f_x /z = \alpha f/z$，表示从相机坐标系到最终像素坐标的直接放缩，跳过中间的像平面。

$$
u = f_x x/z+ c _x ;\
v = f_y y /z+ c_y
$$

内参矩阵：

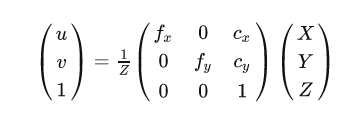
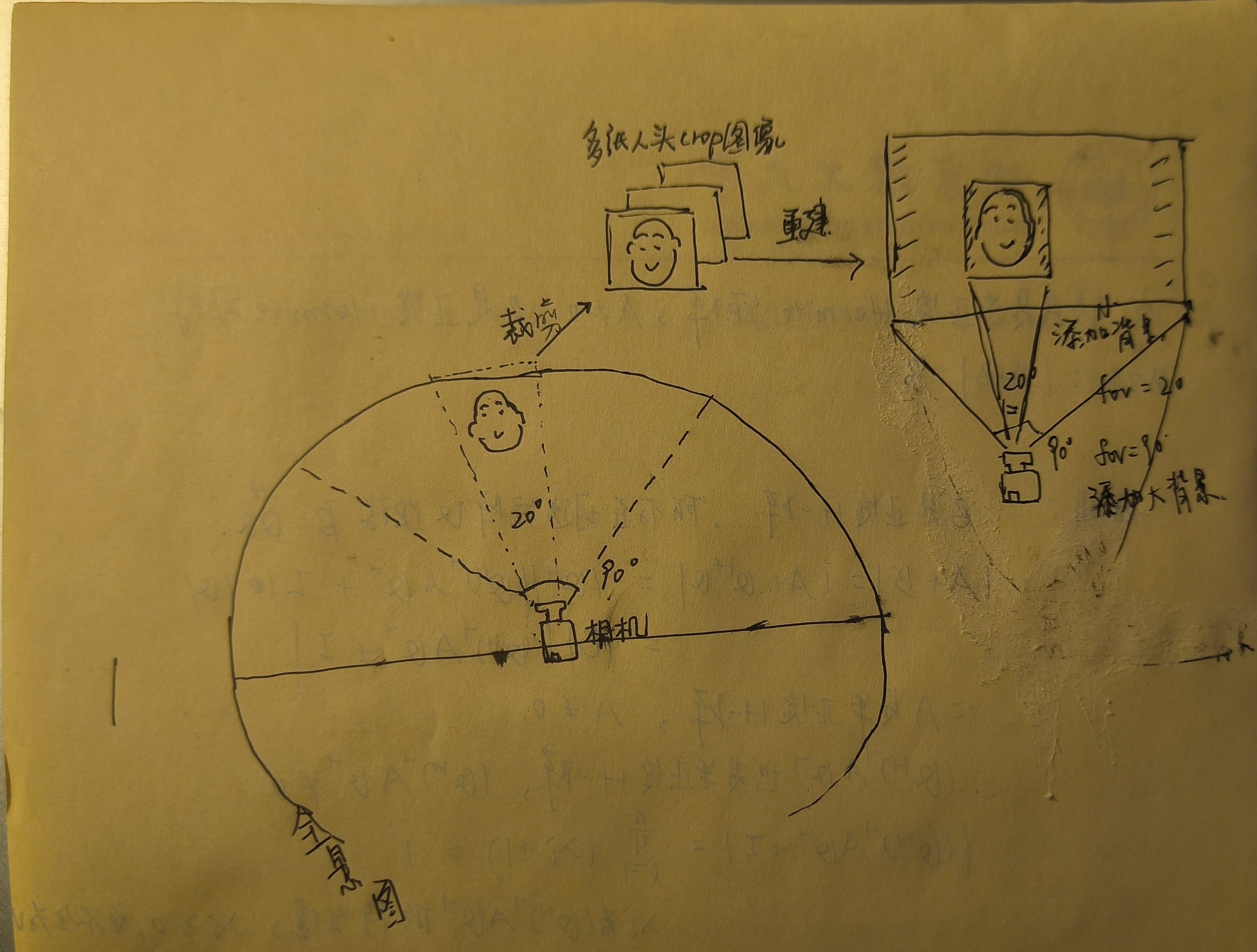
在我们的任务中，相机内参主要用来求视角fov。视角可以从象平面（或像素平面）的高及其到镜头的距离之比求出。这里使用像素平面高的一半$c_y$和深度$f_y$求垂直视角范围：

$$
fov = 2* arctan( c_y / f_y )
$$
实际求出vfov等于20度这样。这样小的fov，从全景图上抠出来的背景包含的内容也会很少，但刚好对应人头的背景大小。而一半人头所占的fov只是原视频中的一部分，原相机完整视频的fov可能是20度的好几倍，如下图所示：

人头坐标系与全景图坐标系的对准

我们定义一个世界坐标系，假设全景图都是在水平面上转360度采集的，那么把全景图直接围在世界坐标系中即可。

在人头重建任务中，人头坐在的坐标系就是世界坐标系。而相机相当于在世界坐标系中游走，带着相机坐标系不断变化。但是，一旦要把人头和背景结合，此时要明确一个问题：全景图所在的世界坐标系才是真正的世界坐标系，将人头放置到全景图环绕的世界中时，人头所在的坐标系自动降格成一个物体坐标系，我称之为“人头坐标系”。

那么此时，就有个五个坐标系。每一级包含下一级：

全景图所在的世界坐标系
- 人头坐标系
  - 相机坐标系
    - 像平面
      - 像素平面

后四个坐标系之间的关系，我们已经通过前面的内参外参矩阵明确了。此时需要明确人头坐标系和世界坐标系之间的关系。此时，我们把重建出的一个人头导入放置好全景图的世界中，发现人头是平躺着、面朝上的：

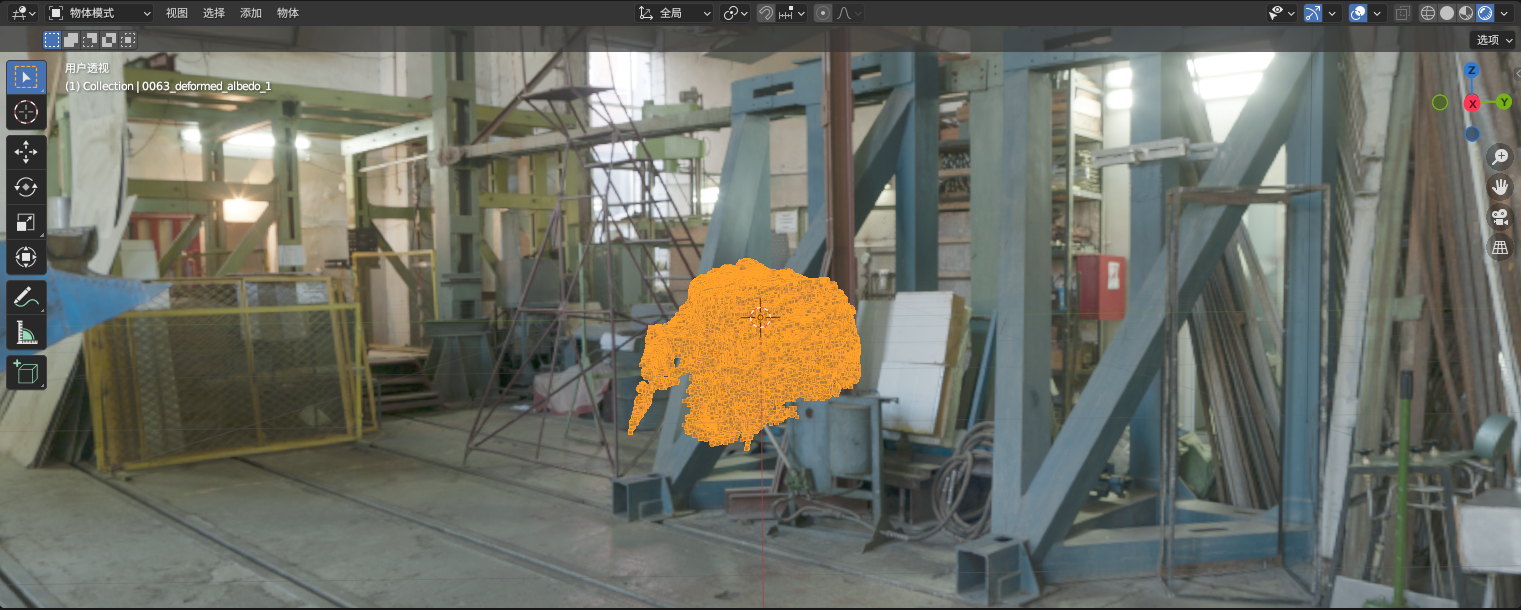
而我们希望人头是正对着我们的。此时，需要对人头坐标系做一个旋转。相对世界坐标系，对人头（人头坐标系）围绕x轴转90度，使其摆正；再围绕z轴旋转90度，使其面向我们。经过两次旋转，在世界坐标系固定为图中（x指出屏幕；y向右；z向上）所示，人头正对着屏幕。

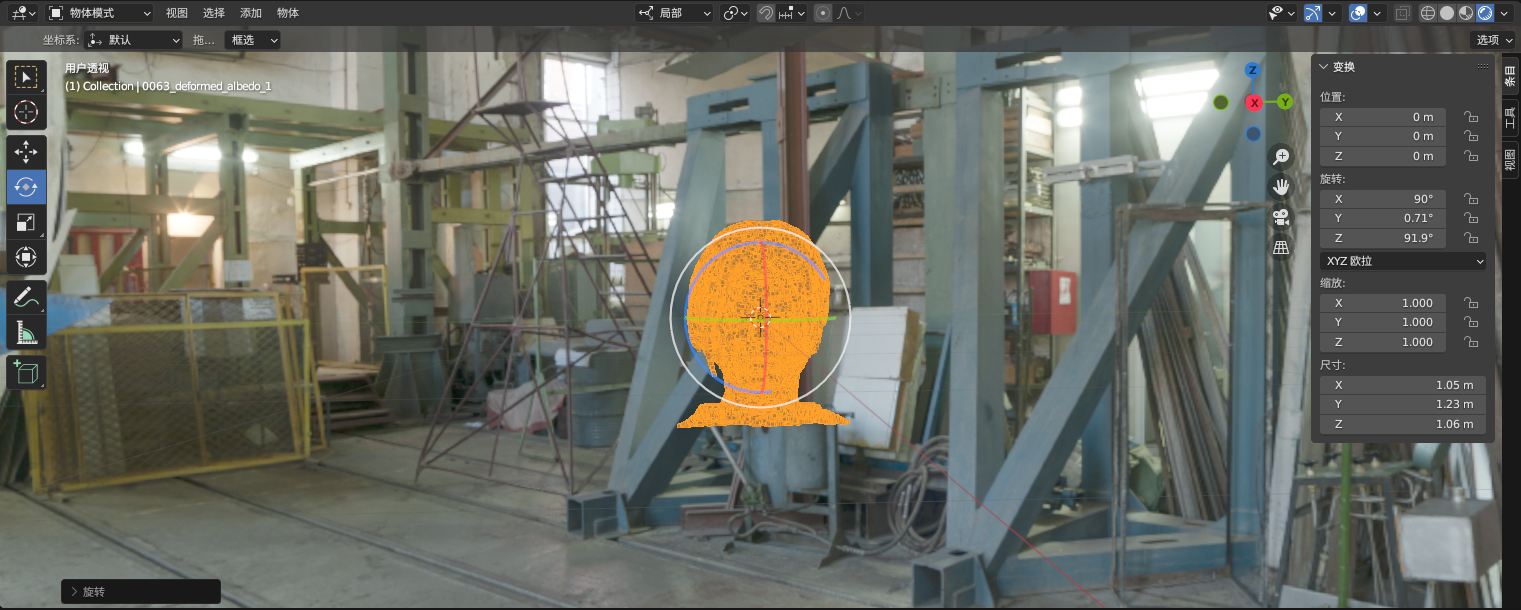
右上角是固定不变的世界坐标系，人头周围的是人头坐标系。
这个旋转其实是把人头坐标系的xyz轴数据当成z-xy。（blender里面铺展全景图的方法和真实的情况有差别，所以看起来是当成zxy）。写成函数：

def headPosition2WorldPosition(position):
    """
    Convert a head position to a world position.
    """
    x, y, z = position

    return np.array([z, -x, y])

推导过程：
右下角是人头在世界坐标系中旋转变换；中部是世界坐标系和全景图之间的变换（blender里对y轴取反，然后再变换并显示的）；上部是旋转矩阵的基本用法。

Secret Garden of Ji

全景图坐标系与人头坐标系的对齐